Zipf’s Law of the Internet: Explaining Online Behavior
In 1949, the linguist George Kingsley Zipf noticed that given a natural language corpus, words are distributed such that the frequency of any word is inversely proportional to its rank in the frequency table. This means that the most frequent word occurs twice as often as the second most frequent word, three times as often as the third most frequent word, etc. He then showed that the relationship also applies to populations in cities of a given country.
An article in The Quarterly Journal of Economics prefaced Zipf’s law for cities as “one of the most conspicuous empirical facts in economics, or in the social science generally.” Social scientists have tried to understand why such a simple relationship holds. Zipf’s Law appears entirely natural. Steven Strogazt wrote in The New York Times, “No city planner imposed it, and no citizens conspired to make it happen. Something is enforcing this invisible law, but we’re still in the dark about what that something might be.”
Zipf’s Law is expressed mathematically as
log R = a – b log n
where R is the rank of the datum, n its value, and a and b are constants.
Data conforms to Zipf’s law when the log-log plot is linear (b is a constant). When this regression is applied to cities, the best fit has been found with b = 1.07.
At Parse.ly, our data shows that the same simple mathematical formulation can be used to explain behavior online. Every day, millions of urls are viewed within the Parse.ly content network; these web pages are published by Mashable, The Atlantic, Gawker, and more than 100 other publishers. A glance at the data on a randomly selected date (March 10, 2013) shows the majority of pageviews in the Parse.ly content network are referred by a small subset of domains on the internet.
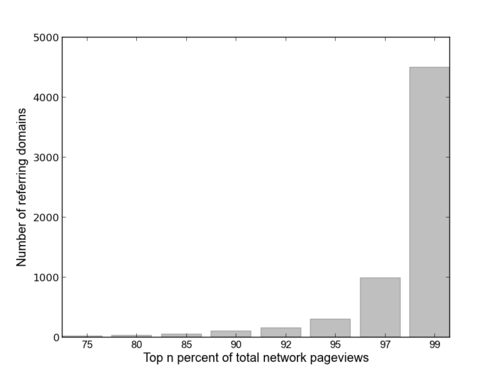
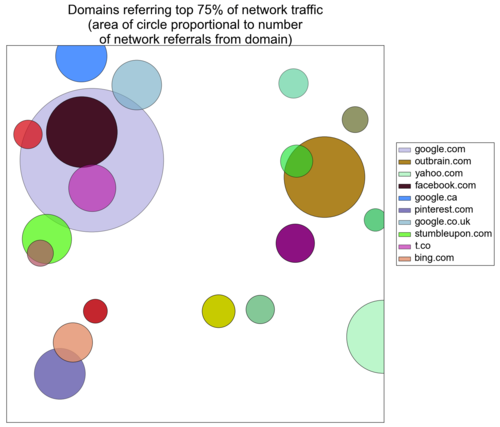
These plots show the ecosystem of domains that referred 75%, 95% and 99% of network traffic on March 10, 2013. Each circle represents a domain and its area is determined by the number of pageviews it referred to the network. Google.com is the lavender body that we like to refer to as the brightest cluster galaxy (BCG) and Facebook is the wine-colored body that is (randomly) superimposed.
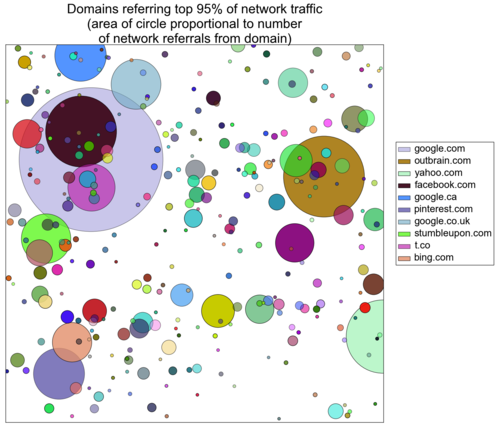
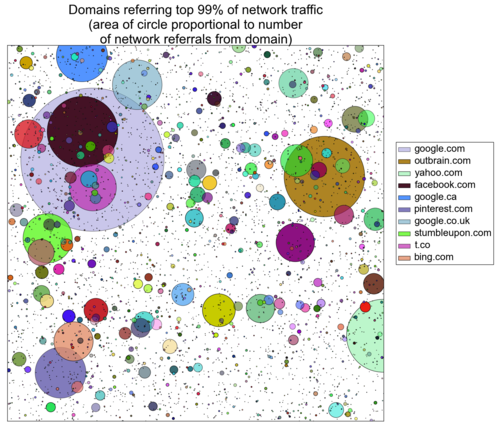
To determine whether the number of network referrals fits a Zipf distribution, we need to measure whether log(pageviews referred) and log(domain rank) are linearly related. A Pearson correlation coefficient equal to (-)1 signifies that two variables have a perfectly linear relationship.
On a log-log scale, we plotted the number of pageviews that each of 50,929 domains referred to the network as a function of how the domain ranked in its number of referrals and found that the Pearson correlation coefficient is -0.988. Inbound traffic to the Parse.ly content network follows a pattern that can be quantified by Zipf’s Law.

A year after Strogazt marveled at the naturally occurring phenomenon of Zipf’s Law of Cities in The New York Times, Edward L. Glaeser, an economics professor at Harvard, posed a hypothesis: “My own view is that Zipf’s Law is really about the operation of agglomeration—the attraction of people to more people.”
We think agglomeration of information—the attraction of people to the richest agglomerations of information—is a starting point to explain Zipf’s Law of the Internet. Inspection of the domains that rank in the top ten on this randomly chosen date and the number of users/voices on each confirms it.
—Emily Chen, Engineering Intern
Want to see more insights on Parse.ly’s network data? Subscribe to The Authority Report.